 |
||
 This page has been mothballed.
This page has been mothballed.
It is no longer being updated but we've left it here for reference.
Geographic Error Modelling
Database Creation
Ordnance Survey (OS) Digital Elevation Models (DEMs) are derived in a two stage process:
- First the contour lines of maps of a particular scale are digitized. Such contour lines are cartographic approximations of the actual heights of the land surface above the ground. Contour lines do not record precise height locations since they are intended to display information at a particular scale. Heights in only a small fraction of the total area of the intended DEM are recorded in this process.
- The values at all other locations are then estimated by an interpolation process. The values are a result of the elevations on the contour lines together with the method used, and the variability of interpolation estimates is well documented elsewhere.
In any large dataset there are liable to be errors, but when the source information (contour lines) covers only a fraction of the total area explicitly and that not precisely, and the remaining values are estimated by a process known to generate particular artefacts and uncertainty, the resulting file (the DEM) must be full of errors.
In this context, as in others of digital spatial information, an error is the deviation between the actual value on the ground and that recorded in the database. It is widely asserted that errors in a particular dataset can be estimated from related observations (similar values) in an independent dataset of higher precision (larger scale), and that is the approach advocated here.
Why Error models?
Given that error occurs in spatial information (as in other information), then we know that it will have an effect on the outcome of any search or analysis of that information deriving values which are not "correct". It is important to establish whether the number of incorrect outcomes in any particular situation is significant for the situation concerned. If it is then the data may not be "fit for use" in the particular context, or it may be possible to generate analyses of the outcome so as to predict the probability of the outcome being correct given the database errors.
Probability prediction can in some data types be defined from standard predictive equations. These have for example been determined for Union and Intersection overlay operations within GIS where the data types input to the analysis are the same (e.g. two zonal coverages) . For such predictive relationships data has to be well behaved, and analyses to proceed predictably. Combining a point (the viewer or viewed point) with a surface (the DEM) to yield a zone (the visible area) is much more complicated and remain a matter for research (but see Huss and Pumar, 1997).
Until such predictive equations are available, if we wish to establish the
effect of database error upon the results of an analysis, then we have to model
the error to yield alternative versions of the data and so derive multiple
versions of the product. In this way, we can examine the effects of different
values of error parameters, and different sources of error.
Error Reporting
Errors are reported for UK DEMs in a global value for all sites. In the documentation for OS 1:50,000 DEM data it is stated that while the accuracy is not tested for all DEM products, where it has been tested the Root Mean Squared Error (RMSE) is between 2 and 3 m. The RMSE is the standard measure of error used by surveyors around the world. It is based on the following formula:
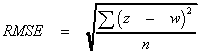
- where z is the elevation recorded in the DEM;
- w is the elevation measured at the higher precision; and
- n is the number of locations tested.
If we make the assumption that the mean error is 0, then this formula is the same as the formula for the standard deviation of the population:
![]()
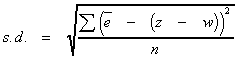
where e is the mean of the errors.
Simple Error Models
The simplest error model can be defined by drawing random values from a normal distribution which has
mean = 0 and s.d = RMSE.
From these we generate a field of white noise which is similar in spatial extent to the DEM and we add that error field to the DEM (Fisher 1991, 1992). The resulting DEM has the essential properties of both the DEM and the error which is known to occur within it. Because the DEM is known to be in error by the amount reported, it can be argued that we actually have a more accurate DEM than we started with. Naturally, however, the error field can be re-populated at any time and another DEM incorporating the error generated.
If a product can be derived from the DEM, such as the visible area, slope, etc. then by repeated derivation of that product over alternative DEMs with different error fields it is possible to derive a set of probable versions of the product. By collecting appropriate statistics from the model we can derive a probable version of the product (Fisher 1992, 1993, 1994).
In the case of the visible area - this is usually presented as a binary area, coded as 0 for out-of-view and 1 for in-view. By adding the visible areas derived from alternative DEMs with different error fields we can derive an estimate of the probability of any location being visible. This is called the Probable Viewshed (Fisher 1993, 1994).
| For a single viewing point a Probable Viewshed derived from the simple error model yields this image: | |
| The following legend is used throughout the illustrations in this paper. A probability of 1 is associated with a dark green, which is not apparent in this view. | |
| It should be compared with the binary viewshed where green indicates in-view: |
We can easily see that the locations immediately around the viewpoint has large probabilities (p = 1), but elsewhere the probability is rarely over 0.5.
This probable viewshed which only is based on the way error is reported (no more information than that is used) does not match our real-world experience as humans, although it may actually be real. If it is it means that the DEM product is dreadful, and that is not the case. The problem is that the error model is too simple. Reporting only the RMSE is not enough.
Spatial Structure in the Error Model
Observe:
- The DEM surface is relatively smooth
- The land surface as it is experienced in the real world is relatively smooth;
- Therefore the difference between them (the error) should also be relatively smooth: it has a spatial structure, a high spatial autocorrelation.
There are a number of ways that spatial structure can be introduced into the error model. The simplest way this can be done is as follows:
- Generate a field of white noise (zero spatial autocorrelation - no spatial structure)
- Determine the spatial autocorrelation of the field
- Swap two values chosen at random
- Recalculate the spatial autocorrelation
- If the spatial autocorrelation has improved (shows increased structure) then retain the swap otherwise reverse it.
- Repeat steps 3 - 5 until the desired spatial autocorrelation is reached.
This simple approach will yield error fields with appropriate mean and standard deviation and with spatial structure.
If this approach is used for error modelling, and desired spatial autocorrelation is set at 0.9 on a scale of -1 to +1 (approximately), and the probable viewshed shown here is derived.
Much of the visible area has a high probability of being seen. This seems to fit out real-world experience, but we are still making three assumptions about the error:
- we are assuming that the mean error is zero
- we have no local information on the RMSE, we are using the national value
- we have no information on the actual spatial structure, the value used in error modelling generates a smooth error field, but is otherwise arbitrary.
Improving Estimation of Error Parameters
Thankfully, all we need to improve the error model for the 1:50,000 DEM is reported by the Ordnance Survey.
On the 1:10,000 maps they give spot heights from ground and aerial survey. By digitizing these spot heights we can compare the values with the 1:50,000 DEM values. These spot heights are:
- Surveyed separately from the map information, being actual heights at a location, and so are independent of the contour maps on which the DEM is based.
- Are not recorded on the 1:50,000 maps and so are not used in construction of those DEMs.
The distribution of spot heights around the Scottish windfarm can be mapped here, as red dots on the greyscale view of the terrain :
At every location it is then possible to subtract the actual values from the DEM values to yield the error at the point.
From this error information we can generate improved location specific error statistics:
- the mean error (which could also be known as the bias); this records systematic error across the dataset;
- the standard deviation of the errors (equivalent to the RMSE, but in this case the actual sample standard deviation without making any assumptions about the mean)
We also have the actual errors at the point, which can be mapped and described here:
From them we can examine the spatial distribution of the errors and apply advanced spatial statistics (geostatistics). We can, for example, see that similar values do cluster within the area. To describing this distribution and generating models of the spatial distribution of the errors.
Actual Error Parameters
Actual Error parameters for the two Scottish DEMs are:
| DEM type | Mean | Standard Deviation | Maximum | Minimum |
|---|---|---|---|---|
| 1:50,000 | 2.1003 | 6.9565 | 28 | -26 |
| 1:10,000 | 0.5089 | 2.6481 | 26 | -11.5 |
The 1:50,000 DEM is seen to have a very real bias in the error, and a large standard deviation. Furthermore, the histogram of the errors shows them to be approximately normally distributed. These results are not necessarily representative. Using the same basic procedure, Monckton (1994) found that the mean and standard deviation of the errors in two areas elsewhere in Britain conformed more closely to the values reported or implied by the OS (mean = 0, RMSE = 2).
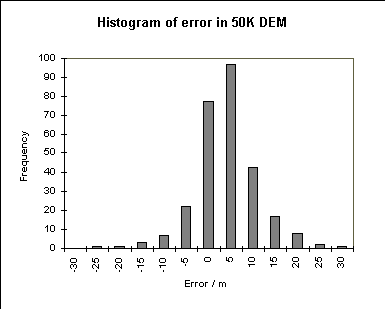
The 1:10,000 DEM is more precise with a mean error of 0.5 and a standard deviation of 2 m, again with a normal distribution. This is a more precise representation of the terrain, as might be hoped in a larger scale database.
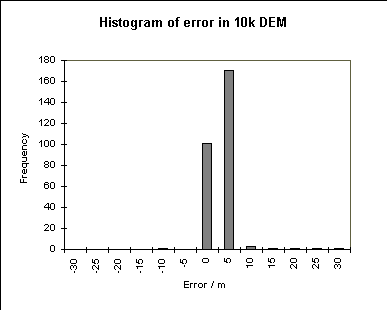
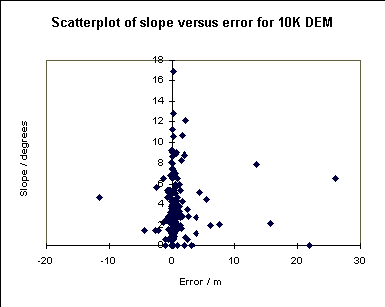
Interestingly, if we compare the error at a point with the slope of the land surface, we can see that for the 1:50,000 DEM there is a significant correlation between the two. This conforms with some ideas about how the error should be distributed. On the other hand, the errors in the 1:10,000 DEM are not correlated to the slope. There is a suggestion here that the spot heights from the 1:10,000 map may have been used in construction of the 1:10,000 DEM, and so are not suitable to test the accuracy of the DEM. If this is the case it is not reassuring to find that the error parameters are in line with those reported by the OS for the 1:50,000 DEM.
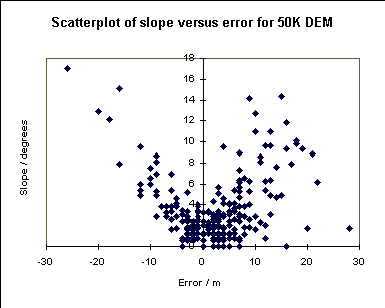
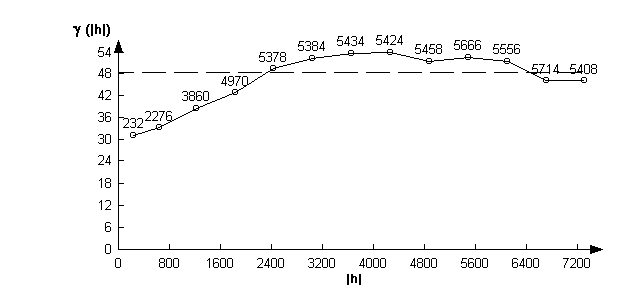
It is also possible to use geostatistics to examine the spatial distribution of the errors. Generating the variogram yields the following figure. This shows the variance between pairs of values at difference spacings, and most importantly, the normally increasing variance with spacing of data pairs. This is observable in the spatial distribution of the error in the 1:50,000 data.
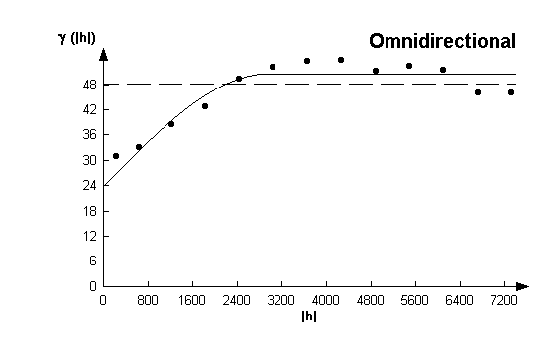
To this variogram we can fit a theoretical variogram. Using the visual interface for curve fitting (Pannitier, 1996), the following diagram is the best fit.
For the 1:10,000 DEM the variogram is rather different, showing as it does no spatial structure (there is no increase of variance with spacing).
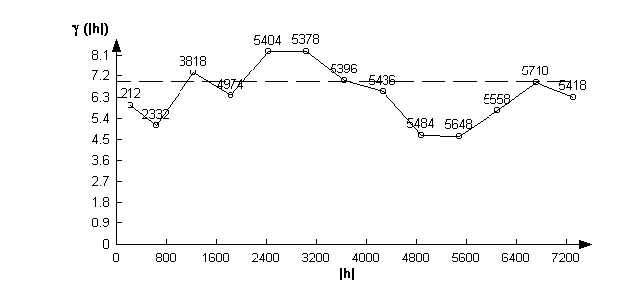
Again this sheds doubt on the independence of the 1:10,000 DEM from the spot heights.
Using the Improved Estimates
We now have a well parameterized description of the error in the 1:50,000 DEM. The description of the 1:10,000 DEM is raising rather more questions than it is answering. If the spot heights are indeed used in creation of the DEM then they are not an appropriate set of data with which to compare the accuracy of that DEM, although they would show something of the process induced error. Rather a further survey at still higher resolution would be required.
We can use the parameterized error for the 1:50,000 DEM constructively to model the error more precisely than before.
This again can be done in a number of ways:
- the actual mean and standard deviations of the error can be used in generating the noise fields;
- point of known error can be included as fixed points in the error fields; and
- simulating error with spatial structure can involve keeping the locations of known error to that error value.
Sequential simulation, a process in the geostatistical toolkit can accomplish all these. It requires as input a model variogram, such as that shown above. Alternatively the method outlined above for generating spatially autocorrelated error fields can be used, and the locations of known error never changed. This increases the computation time, but improves the error model enormously.
This third version of the probable viewsheds look like this:
Wind Turbines
Looking at the union of all 48 sites identifying the wind farm, we can yield see the differences between the patterns generated by the different error models more strikingly. In this instance the elevation at the turbines is 25 m (about half way up the turbine), and the viewer elsewhere is 2 m above the ground.
| The binary viewshed is shown in pink with the wind turbine sites marked by crosses: | The probability of any location being able to see the turbine masts is shown in this image, from the simplest error model (when RMSE = 2). | The probability of being able to see the mast when only the spatial structure is incorporated is shown here: |
| Using an arbitrary spatial structure, but mean and standard deviation of the actual errors it looks like this: | When the error locations are also included as fixed values (the most complex error model) it probability looks like this: | |
We can see that:
- with the simplest error model we badly underestimate the probabilities;
- with only spatial structure included in the error model the estimates are likely to be too great;
- the final two maps both provide more acceptable estimates with large but not excessive areas with high probability, and an extensive area with lower probabilities. The two are only a little different, indicating that it may not be necessary to incur the increased computing cost of using the fixed locations.
Visualisation
In the context of wind turbines, the issue of visualization of the probable visible areas should also be addressed. An interactive visualization is shown. A representation of a turbine on one side is live and when clicked the probable area visible changes to show the area which can probably see to that height. Two different models are shown reflecting the spatial structure without actual errors and that with actual errors.
Conclusion
Increasing complexity in the error model has been shown.
The increase in complexity has yielded increasingly plausible results with defensible methods yielding results which show a compromise between our own world experience and the quality of the database used. In some situations the second model (with simulated spatial structure) may suffice, but only when the error parameters for the actual area conform to the description of error provided by the data supplier.
To use error estimates in developing realistic models of error so that those errors can be propagated into non-trivial spatial operations requires a complete description of the statistical and spatial distribution of the errors. The best way to do that is not for the data providers to give still more estimates of global parameters, but to provide well surveyed data points of higher precision than the database itself. Many data providers already hold those higher precision data, and merely need to make them available.
The probable viewsheds which result in this process are completely plausible. Field verification has not been attempted, but because the probability relates to the database error, and nothing in the field, it is not readily apparent how it would be done. General checks might be made that areas with high probability can indeed see to the locations described, but that is not simple, and it is not entirely clear how to evaluate the results. Verification of the probabilities awaits further investigation. In the meantime, estimation of the probabilities based on a spatially distributed model of error is essential, and at present the best method has been presented here.
References
Fisher, P.F., 1991. First experiments in viewshed uncertainty: the accuracy of the viewable area. Photogrammetric Engineering and Remote Sensing, 57, 1321-1327.
Fisher, P.F., 1992. First Experiments in viewshed uncertainty: simulating the fuzzy viewshed. Photogrammetric Engineering and Remote Sensing, 58, 345-352.
Fisher, P.F., 1993, Algorithm and implementation uncertainty in viewshed analysis. International Journal of Geographical Information Systems 7 (4): 331-374
Fisher, P.F., 1994, Probable and fuzzy models of the viewshed operation. In: M.Worboys (editor), Innovations in GIS 1 (Taylor & Francis, London) pp 161-175.
Huss R.E., and Pumar, M.A., 1997. Effect of database erors on intervisibility estimation. Photogrammetric Engineering and Remote Sensing, 63: 415-424
Monckton, C.G., 1994. An investigation into the spatial structure of error in digital elevation data. In M.Worboys (ed) Innovations in GIS 1, Taylor & Francis, London, pp201-211
Pannatier, Y, 1996, Variowin: Software for spatial data analysis in 2D. Springer-Verlag, New York.
Sorensen, P., and Lanter, D., 1993, Two algorithms for determining partial visibility and reducing data structure induced error in viewshed analysis. Photogrammetric Engineering and Remote Sensing, 59 (7): 1129-1132
|
Updated: 23 January 2024
|
